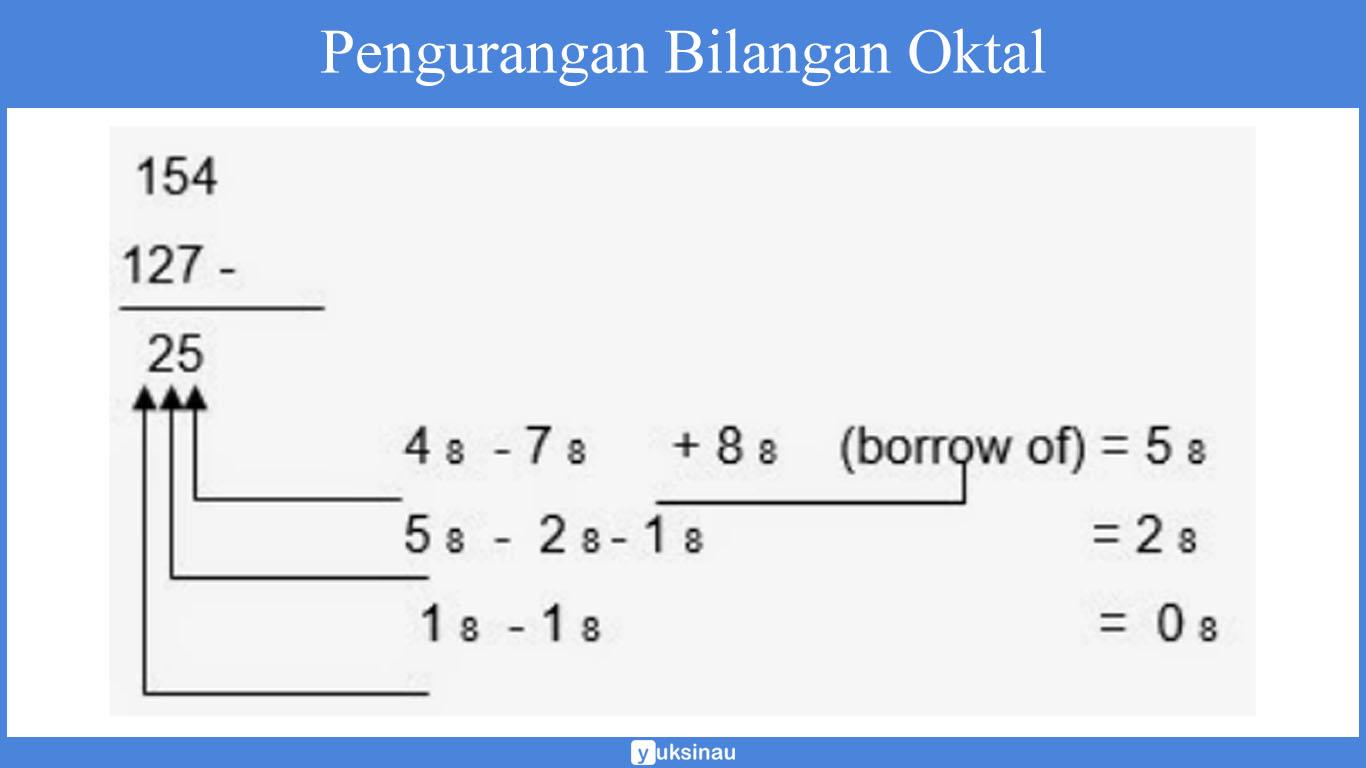
1. FSA ( Finite State Automata )
Finite State Machine dapat berupa suatu mesin yang tidak memilikioutput. Finite State Machine yang tidak mengeluarkan output ini dikenal sebagai Finite State Automata(FSA).
Pada FSA mesin mula-mula dalam state S0 dan menerima sederatan masukan yang dapat mengubahnya ke state-state berikutnya. Dalam FSAjuga dikenal himpunan state-state tertentu yang disebut sabagai FINALSTATE. Perubahan dari satu state ke state berikutnya mengikuti sturantertentu yang dirumuskan sebagai suatuFUNGSI transisi M.
FSA didefinisikan sebagai pasangan 5 Tupel → M = (Q, ∑, δ, S, F).
Keterangan :
Q : Himpunan hingga state.
∑ (Sigma) : Himpunan hingga simbol input (alfabet).
δ (Delta) : Fungsi transisi, menggambarkan transisi state FSA akibat pembacaan simbol input. Biasanya fungsi transisi ini digambarkan dalam bentuk tabel.
S ∈ : State awal.
F ⊆ : Himpunan state akhir.
FSA terbagi menjadi dua jenis, yaitu :
1. Deterministic Finite Automata
Artinya: Dari suatu state ada tepat satu state berikutnya untuk setiap simbol input yang diterima.
2. Non Deterministic Finite Automata (NDFA) / NFA
Artinya: Dari suatu state bisa terdapat 0,1 atau lebih busur keluar (transisi) berlabel simbol input yang sama.
Contoh I :
Buatlah diagram transisi dari FSA yang didefinisikan sebagai :
M = (K, VT, M, S, Z) dimana :S ={S0, S1, S2, S3}VT ={ 0,1 }K ={S0 , S3}
Dengan fungsi transisi M ada pada tabel transisi sebagai berikut :

Diagram Transisi :

Cara kerja FSA :
Mula-mula dalam state S0
Jika dari S0 menerima 1 : akan ke State-S1
Jika dari S0 menerima 11 : akan ke State-S1 lalu ke S2
Jika dari S0 menerima 0 : akan tetap di State- S0
Jika dari S0 menerima 10 : akan tetap kembali lagi State- S0
Jika dari S0 berturut-turut menerima masukan : 111, maka ia akan kembali ke- S0
Contoh II :
Seorang petani dengan seekor serigala, kambing dan seikat rumput berada pada suatu sisi sungai. Tersedia hanya sebuah perahu kecil yang hanya dapat dimuati dengan petani tersebut dengan salah satu serigala, kambing atau rumput. Petani tersebut harus menyeberangkan ketiga bawaannya kesisi lain sungai. Tetapi jika petani meninggalkan serigala dan kambing pada suatu saat, maka kambing akan dimakan serigala. Begitu pula jika kambing ditinggalkan dengan rumput, maka rumput akan dimakan oleh kambing. Mungkinkah ditemukan suatu cara untuk melintasi sungai tanpa menyebabkan kambing atau rumput dimakan.


FSA Sebagai Pengenal String
Mesin FSA tersebut jika menerima masukan sederetan simbol dari simbol-simbol yang diijinkan maka akan menuju suatu state tertentu. Jika state akhir yang ditempuh setelah suatu FSA menerima sederetan simbol adalah state final, maka deretan simbol (string) tersebut dikatakan dikenali oleh FSA, atau dengan kata lain FSA mengenali string tersebut.
String yang dikenali oleh FSA merupakan suatu bahasa yang dikenali oleh FSA tersebut. Jika dimiliki FSA M maka bahasa yang dikenali oleh FSA di notasikan sebagai :
L(M) = { x | x semua string yang mengantar M dari S0 ke (Si ϵ Z) }
Untuk mesin FSA pada contoh :
L(M) = { 0* , 0*(10)0* , 0*(110,111)0* }
Contoh :
Tentukan bahasa L(M) yang dikenali oleh Mesin M berikut ini :

Jawab :
Dari diagram terlihat bahwa final-state adalah S3. Pergerakan state yang mengantar ke final state adalah S0 S1 S2 S3 yakni string : 011 atau string 111 yang dapat ditulis sebagai (0,1)11.
Pergerakan yang lain adalah dari S0 langsung ke S2 yaitu : S0 S2 S3 yang dilakukan melalui string : 01 Setelah berada pada final state masih ada pergerakan yang bersifat rekursif pada S3 yaitu apabila diberikan masukan 0,00,000,… atau : 0*.
Dengan demikian jika seluruh string tersebut digabungkan akan menjadi : (0,1)110* U 010*, sehingga bahasa yang dikenali adalah : L(M)= { (0,1)110* U 010* } = { ((0,1)11 U 01)0* }
2. DFA (DETERMINISTIC FINITE AUTOMATA)
Deterministic Finite Automata (DFA) → M = (Q, ∑, δ, S, F), dimana :
Q : Himpunan state/kedudukan
∑ (Sigma) : Himpunan simbol input
δ (Delta) : Fungsi transisi, dimana δ ∈ Q x ∑ → Q
S ∈ : State awal (initial state)
F ⊆ : Himpunan state akhir (final state)
Language → L(M) : (x | δ (S,x) di dalam F)
Pada DFA, untuk karakter input tertentu, mesin hanya menuju satu state. Fungsi transisi didefinisikan pada setiap state untuk setiap simbol input. Dan juga di DFA null (atau ε) pemindahan tidak diizinkan, DFA tidak dapat mengubah state tanpa karakter input apa pun.
Contoh :
Diketahui DFA :
Q = {q0, q1, q2}
∑ = {a, b}
S = q0
F = {q0, q1}
δ diberikan dalam tabel berikut :

Ilustrasi graf untuk DFA F sebagai berikut :

Penelusuran/Tracing :
Telusurilah, apakah kalimat-kalimat berikut diterima DFA : abababaa, aaaabab, aaabbaba.
Jawab :
M(q0,abababaa) → M(q0,bababaa) → M(q1,ababaa) → M(q0,babaa) → M(q1,abaa) → M(q0,baa) → M(q1,aa) → M(q0,a) → q0
Tracing berakhir di q0 (stata penerima) → kalimat abababaa diterima
M(q0,aaaabab) → M(q0,aaabab) → M(q0,aabab) → M(q0,abab) → M(q0,bab) → M(q1,ab) → M(q0,b) → q1
Tracing berakhir di q1 (stata penerima) → kalimat aaaababa diterima
M(q0,aaabbaba) → M(q0,aabbaba) → M(q0,abbaba) → M(q0,bbaba)→ M(q1,bbaba) → M(q2,baba) → M(q2,aba) → M(q2,ba) → M(q2,a) → q2
Tracing berakhir di q2 (bukan stata penerima) --> kalimat aaabbaba ditolak
Simpul Singkat : Sebuah kalimat diterima oleh DFA di atas jika tracingnya berakhir di salah satu state akhir.
3. NDFA/NFA (NON DETERMINISTIC FINITE AUTOMATA)
Non Deterministic Finite Automata (NFA) → M = (Q, ∑, δ, S, F), dimana :
Q : Himpunan state/kedudukan
∑ (Sigma) : Himpunan simbol input
δ (Delta) : Fungsi transisi, dimana δ ∈ Q x (∑ ⋃ ε) → P(Q)
P(Q) : set of all subsets of Q
S ∈ : State awal (initial state)
F ⊆ : Himpunan state akhir (final state)
Language → L(M) : (x | δ (S,x) di dalam F)
Contoh :
Berikut ini sebuah contoh NFA (Q, ∑, δ, S, F). dimana :
Q = {q0, q1, q2, q3, q4}
∑= {a, b,c}
S = q0
F = {q4}
δ diberikan dalam tabel berikut :

Digram Transisi yang dapat dibuat :

L(M) = {aabb,...}
Sebuah kalimat di terima NFA jika :
Salah satu tracing-nya berakhir di state akhir, atau himpunan state setelah membaca string tersebut mengandung state akhir.
Penelusuran/Tracing :
Telusurilah, apakah kalimat-kalimat berikut diterima NFA di atas :
ab, abc, aabc, aabb
Jawab :
δ(q0 ,ab) ⇒ δ(q0,b) ∪ δ(q1 ,b) ⇒ {q0, q2} ∪ {q1} = {q0, q1, q2}
Himpunan state tidak mengandung state akhir ⇒ kalimat ab tidak diterima
δ(q0, abc) ⇒ δ(q0, bc) ∪ δ(q1, bc) ⇒ {δ(q0, c) ∪ δ(q2, c)} ∪ δ(q1, c)
{{q0, q3} ∪ {q2}} ∪ {q1} = {q0, q1, q2, q3}
Himpunan state tidak mengandung state akhir ⇒ kalimat abc tidak diterima
δ(q0, aabc) ⇒ δ(q0, abc) ∪ δ(q1, abc) ⇒ {δ(q0, bc) ∪ δ(q1, bc)} ∪ δ(q1, bc)
⇒ {{δ(q0, c) ∪ δ(q2, c)} ∪ δ(q1, c)} ∪ δ(q2, c)
⇒ {{{q0, q3} ∪ {q2}} ∪ {q1}} ∪ {q1} = {q0, q1, q2, q3}
Himpunan state tidak mengandung state akhir ⇒ kalimat aabc tidak diterima
δ(q0, aabb) ⇒ δ(q0,abb) ∪ δ(q1, abb) ⇒ {δ(q0, bb) ∪ δ(q1, bb)} ∪ δ(q1, bb)
⇒ {{δ(q0, b) ∪ δ(q2, b)} ∪ δ(q1, b)} ∪ δ(q1, b)
⇒ {{{q0, q2} ∪ {q2, q4}} ∪ {q1}} ∪ {q1} = {q0, q1, q2, q4}
Himpunan state mengandung state akhir ⇒ kalimat aabb diterima
4. EKUIVALEN ANTAR DFA
Dua buah DFA dikatakan equivalen jika keduanya dapat menerima bahasa yang sama. Misalkan kedua DFA tersebut adalah A dan A’. Misalkan pula bahasa yang diterima adalah bahasa L yang dibangun oleh alfabet VT = {a1, a2, a3, ..., an}. Berikut ini algoritma untuk menguji equivalensi dua buah DFA.
1) Berikan nama kepada semua stata masing-masing DFA dengan nama berbeda. Misalkan nama nama tersebut adalah : S, A1, A2, ... untuk DFA A, dan : S’, A1’, A2’, ... untuk DFA A’.
2) Buat tabel (n+1) kolom, yaitu kolom-kolom : (v, v’), (va1, va1’), ..., (van, van’), yaitu pasangan terurut (stata DFA A, stata DFA A’).
3) Isikan (S, S’) pada baris pertama kolom (v, v’), dimana S dan S’ masing-masing adalah stata awal masing-masing DFA.
4) Jika terdapat edge dari S ke A1 dengan label a1 dan jika terdapat edge dari S’ ke A1’ juga dengan label a1, isikan pasangan terurut (A1, A1’) sebagai pada baris pertama kolom (va1, va1’) Lakukan hal yang sama untuk kolom-kolom berikutnya.
5) Perhatikan nilai-nilai pasangan terurut pada baris pertama. Jika terdapat nilai pasangan terurut pada kolom (va1, va1’) s/d (van, van’) yang tidak sama dengan nilai pasangan terurut (v, v’), tempatkan nilai tersebut pada kolom (v, v’) baris-baris berikutnya. Lakukan hal yang sama seperti yang dilakukan pada langkah (4). Lanjutkan dengan langkah (5).
6) Jika selama proses di atas dihasilkan sebuah nilai pada kolom (v, v’), dengan komponen v merupakan stata penerima sedangkan komponen v’ bukan, atau sebaliknya, maka kedua DFA tersebut tidak ekuivalen. Proses dihentikan.
7) Jika kondisi (6) tidak dipenuhi dan jika tidak ada lagi pasangan terurut baru yang harus ditempatkan pada kolom (v, v’) maka proses dihentikan dan kedua DFA tersebut ekuivalen.
Contoh :
Periksalah ekuivalensi kedua DFA berikut :

Jawab :
Dengan menggunakan algoritma di atas maka dapat dibentuk tabel berikut,

Keterangan :
> (2, 5) adalah pasangan terurut baru
> (3, 6) adalah pasangan terurut baru
> (4, 7) adalah pasangan terurut baru
> tidak ada lagi pasangan terurut baru
5. REDUKSI JUMLAH STATE
Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi). State pada FSA dapat direduksi apabila terdapat useless state. Hasil dari FSA yang direduksi merupakan ekuivalensi dari FSA semula. Pasangan State dapat dikelompokkan berdasarkan:
1. Distinguishable State yang artinya dapat dibedakan. Dua state p dan q dari suatu DFA dikatakan indistinguishable apabila :
δ(q,w) ∈ F dan δ(p,w) ∈ F atau δ(q,w) ∉ F dan δ(q,w) ∉ F
2. Indistinguishable State yang artinya tidak dapat dibedakan.
Dua state p dan q dari suatu DFA dikatakan distinguishable apabila :
Ada string w ∈ S* hingga δ(q,w) ∈ F dan δ(p,w) ∉ F
Relasi :
Pasangan dua buah state memiliki salah satu kemungkinan : distinguishable atau indistinguishable tetapi tidak kedua-duanya.
Dalam hal ini terdapat sebuah relasi :
Jika p dan q indistinguishable,
dan q dan r indistinguishable
maka p, r indistinguishable
dan p,q,r indistinguishable
Dalam melakukan eveluasi state, didefinisikan suatu relasi :
Untuk Q yg merupakan himpunan semua state
D adalah himpunan state-state distinguishable, dimana D Ì Q
N adalah himpunan state-state indistinguishable, dimana N Ì Q
maka x Î N jika x Î Q dan x ∉ D
Langkah :
Hapuslah semua state yg tidak dapat dicapai dari state awal (useless state)
Buatlah semua pasangan state (p, q) yang distinguishable, dimana p ∈ F dan q ∉F. Catat semua pasangan-pasangan state tersebut.
Cari state lain yang distinguishable dengan aturan: “Untuk semua (p, q) dan semua a ∈ ∑, hitunglah δ (p, a) = pa dan δ (q, a) = qa” Jika pasangan (pa, qa) adalah pasangan state yang distinguishable maka pasangan (p, q) juga termasuk pasangan yang distinguishable.
Semua pasangan state yang tidak termasuk sebagai state yang distinguishable merupakanstate-state indistinguishable.
Beberapa state yang indistinguishable dapat digabungkan menjadi satu state.
Sesuaikan transisi dari state-state gabungan tersebut.
Contoh :
Sebuah Mesin DFA

Sumber :
https://docplayer.info/36555908-Teori-bahasa-dan-automata-finite-state-automata-non-finite-state-automata.html
Alif Muhammad Akmal
1810631170212
Alif Muhammad Akmal
1810631170212

















 Lalu
Lalu